热机是将热能转化为机械能的装置,也是理解非平衡态热力学的重要模型系统。在实际应用中,人们既希望热机能够高效工作(高效率,热功转换比高),又希望它能够以高功率快速工作(单位时间输出功多)。然而,这两个目标之间存在着由不可逆耗散导致的矛盾。卡诺效率作为热机效率的理论上限,传统上被认为只能在准静态可逆循环中实现,此时系统的功率为零。这就导致了所谓的“功率-效率权衡”问题:当试图提高热机的功率时,必然会损失一定的效率。这个权衡关系已经被证明在多种情况下都是普适的,特别是在低耗散热机中,热机以最大功率运行时的效率(最大功率效率)有着明确的上限。
近日,物理与天文学院讲师马宇翰与德累斯顿系统生物中心的博士后研究员梁师翎(物理学系2018届本科毕业生,2024年博士毕业于瑞士洛桑联邦理工学院)等合作提出了一个做功物质具有能级简并度的最小生化热机模型[图1(a)]。该热机在最大功率下的效率可以突破低耗散热机的普适上限,并在热力学极限下逼近卡诺效率[图1(b)]。这一发现表明,简并度这一内禀物理量可以作为一种热力学资源,帮助我们突破传统的功率-效率权衡限制。这项研究的另一个重要发现是关于功率效率权衡的普适性。在卡诺效率较小对应的线性响应区域,最大功率下的效率与卡诺效率之比通常为二分之一,这被称为“1/2普适性”。然而,研究发现这个普适性在大简并度极限下会被打破。卡诺效率(由环境温差决定)和简并度(由系统尺寸和相互作用具体形式确定)的极限次序会影响最大功率效率关于卡诺效率的比例系数[图1(c)]。这说明,当系统具有发散的内禀量时,一些传统的热力学限制可能需要重新审视。
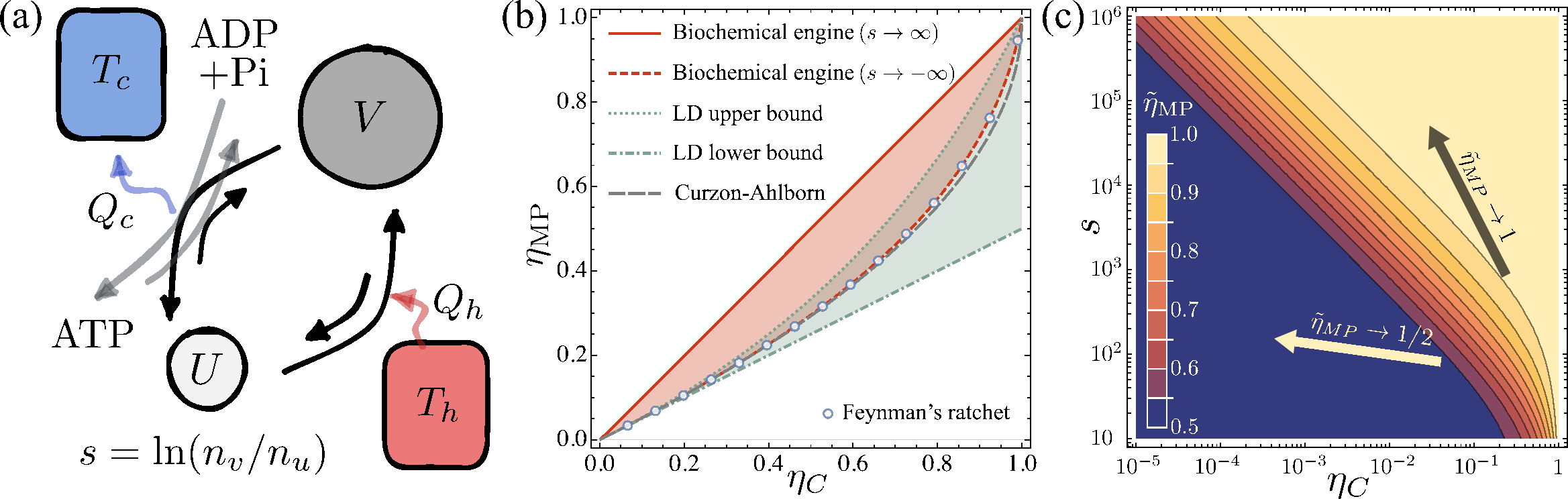
图1
图 1(a) 生化热机最小模型,包含两个能级U和V,分别与冷热两个温度为Tc和Th的热库耦合。系统可以通过ATP合成和自发跃迁两种方式在能级间转换,两个能级的简并度之比由s = ln(nv/nu)表示。(b) 热机的最大功率效率(ηΜP)与卡诺效率(ηC)的关系。红色实线和虚线分别表示简并度s趋于正负无穷时的效率。热机效率可以突破低耗散热机的效率上限(绿色虚线),在s趋于无穷时达到卡诺效率。(c)颜色图展示了归一化的最大功率效率如何随简并度和卡诺效率变化。在不同极限顺序下,系统表现出从普适的1/2卡诺效率到卡诺效率的连续转变。
本研究揭示了如何通过调控做功物质的内禀性质来改善热机性能,而不是通过设计热机循环的操作过程这一常规的优化方式。该工作不仅深化了我们对非平衡热力学的理解,也为能源技术的发展提供了新的思路。研究的未来将继续探索更复杂的多能级系统,研究简并度与其他集体效应的相互影响。这种理论框架有望为设计新型高效能量转换装置提供指导。通过合理设计系统的内部自由度和能级结构,我们可能发现更多突破传统热力学限制的新途径。随着实验技术的发展,这些理论预言的实验验证也将成为值得探索的研究方向。
相关研究论文于2025年1月13日以“Minimal Model for Carnot Efficiency at Maximum Power”为题在线发表在国际权威期刊Physical Review Letters上[Phys. Rev. Lett. 134, 027101 (2025)]。德累斯顿系统生物中心的博士后梁师翎为论文第一作者,梁师翎和北京师范大学物理与天文学院讲师马宇翰为共同通讯作者,文章的其他合作者有德国马普所复杂系统物理研究所的Daniel M. Busiello以及瑞士洛桑联邦理工学院的Paolo De Los Rios。该工作得到瑞士国家科学基金会(SNSF) 、日本学术振兴会 (JSPS)、国家自然科学基金青年基金、北京市自然科学基金以及中央高校基本业务经费的资助。
论文链接:https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.134.027101