近日,物理学系艾清课题组和南方科技大学鲁大为课题组在量子精密测量领域取得重要进展,实验实现了由量子芝诺效应增强的量子精密测量。南方科技大学博士生龙新月、北京师范大学博士生何宛亭和重庆邮电大学张娜娜讲师为该论文的共同第一作者。其他合作者还包括南方科技大学李俊研究员和辛涛副研究员等。
对量子系统的测量精度,以光学上的拉姆齐干涉仪为例,传统的方法是将初态制备到叠加态上,让其在系统哈密顿量下演化,随后测量末态,重复测量n次,不确定度将正比于n-1/2,这就是标准量子极限(Standard Quantum Limit, SQL)。为了提高测量精度,将初态制备为n量子比特最大纠缠态(纠缠探针),经过同样演化后测量末态,得到的不确定度正比于n-1,即海森堡极限(Heisenberg Limit),也是量子力学规定的精度上限。然而,任何量子系统都不可避免地与环境存在相互作用,这会导致退相干、振幅衰减、退极化等效应,使得测量精度无法达到海森堡极限,导致量子纠缠态提供的测量优势失效。

图1:拉姆齐干涉仪
当量子系统演化时,环境噪声如果等价于对系统的频繁观测,就会导致系统停留在原来的状态上,这与“芝诺悖论”有异曲同工之妙,因而也被称之为量子芝诺效应(Quantum Zeno Effect)[8,9]。根据是否具有记忆效应,噪声可分为马尔可夫和非马尔可夫噪声。马尔可夫噪声不具有记忆效应,而真实的物理环境通常带有一定的非马尔可夫性。2012年,Chin, Huelga和Plenio [2,3] 在理论上证明了在非马尔可夫噪声中,纠缠探针可以超过标准量子极限的精度,达到n-3/4。这被称为芝诺极限,其关键思想是量子芝诺效应可以显著降低退相干误差。然而,用实验验证Chin的理论有两个主要挑战。首先,利用量子芝诺效应提高量子精密测量的精度,需要知道完整的系统与环境相互作用信息,这对实验提出了很大的挑战。其次,要证实测量精度能否有n1/4倍的提升,需要相对较大的量子比特资源,这也加大了实验的难度。
为了解决这两个难题,研究者采用课题组最新开发的量子模拟方法[5-7]来调制噪声模型,并应用bath-engineering技术来模拟高精度的非马尔可夫环境。类似于经典的拉姆齐干涉,首先将初始态制备到叠加态,然后让其在经过时间调制的随机哈密顿量下演化。Bath-engineering的核心就是在初始的时候制备大量相同的初态,并让它们在不同的随机哈密顿量下演化一段时间,将末态进行系综(时间)平均,理论上就可以模拟纯退相干环境。我们在核磁共振量子模拟器上进行实验,环境调制是通过使用多达7个核自旋量子比特来实现的。在保证纠缠探针的高保真初始化和读出的情况下,我们观察到,使用纠缠探针,目标磁场的计量精度正好增强了n1/4倍,达到了QZE极限。此外,我们设置了一组没有噪声的对照实验,证明纠缠探针能达到海森堡极限,也即使得计量精度增强n1/2倍。这些实验为纠缠增强的量子计量学问题建立了一套完整的实验体系。
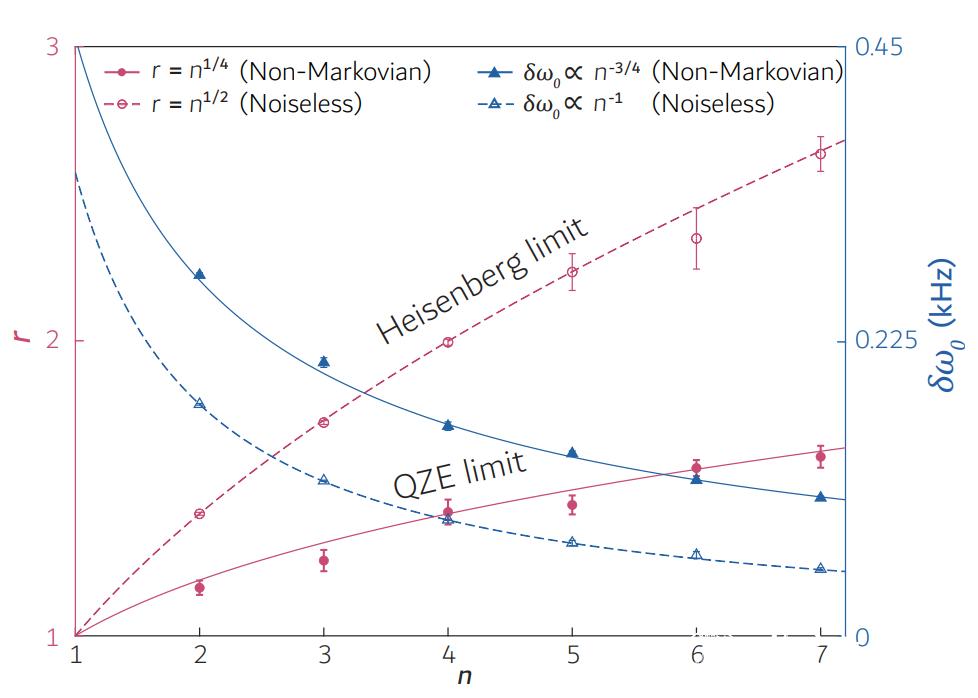
图2:非马尔可夫噪声和无噪声环境下的实验结果。利用纠缠探针,非马尔可夫噪声下的测量精度随着比特数n的提升实现了n1/4倍的增强,而无噪声环境下(对照实验)则达到了n1/2倍的增强。
在这项工作中,研究者应用了一种无需辅助量子比特的bath-engineering技术, 节省了量子比特资源。同时,实验过程只要求单量子比特绕z轴旋转的操作集合, 也易于扩展到其他物理体系。我们的实验不仅是对Chin理论的证明,也为在其它量子系统中实现非马尔可夫动力学提供了工具,为探索其它系统中的噪声环境下的量子精密测量铺平了道路。
研究成果以“Entanglement-Enhanced Quantum Metrology in Colored Noise by Quantum Zeno Effect”为题发表在物理学期刊《物理评论快报》上。该课题由艾清副教授和鲁大为副教授联合指导,前期由硕士生邓汝琼通过理论计算验证了方案的可行性,由博士生龙新月、何宛亭、张娜娜制定实验方案,龙新月完成实验,最后由何宛亭、张娜娜、龙新月进行理论拟合。该工作得到了北京市自然科学基金、北京师范大学、科技部、国家自然科学基金委、广东省科技厅、深圳市科创委和南方科技大学等部门的大力支持。
参考文献:
1. Entanglement-Enhanced Quantum Metrology in Colored Noise by Quantum Zeno Effect, X.-Y. Long, W.-T. He, N.-N. Zhang, K. Tang, Z.-D. Lin, H.-F. Liu, X.-F. Nie, G.-R. Feng, J. Li, T. Xin, Q. Ai, and D. W. Lu, Phys. Rev. Lett. 129, 070502 (2022)
2. Quantum Metrology in Non-Markovian Environments, A.W. Chin, S. F. Huelga, and M. B. Plenio, Phys. Rev. Lett. 109, 233601 (2012)
3. Magnetic Field Sensing beyond the Standard Quantum Limit under the Effect of Decoherence, Y. Matsuzaki, S. C. Benjamin, and J. Fitzsimons, Phys. Rev. A 84, 012103 (2011)
4. Improvement of Frequency Standards with Quantum Entanglement, S. F. Huelga, C. Macchiavello, T. Pellizzari, A. K. Ekert, M. B. Plenio, and J. I. Cirac, Phys. Rev. Lett. 79, 3865 (1997)
5. Quantum Coherence Effects in Photosynthesis and Their Quantum Simulation, N.-N. Zhang, W.-T. He, Z.-H. Sun, R.-Q. Deng, Y.-Y. Wang, and Q. Ai, Sci. China Phys. Mech. 52, 270011 (2022)(校庆特邀综述)
6. Efficient Quantum Simulation of Open Quantum Dynamics at Various Hamiltonians and Spectral Densities, N.-N. Zhang, M.-J. Tao, W.-T. He, F.-G. Deng, N. Lambert, and Q. Ai, Front. Phys. 16, 51501 (2021)
7. Efficient Quantum Simulation of Photosynthetic Energy Transfer, B.-X. Wang, M.-J. Tao, Q. Ai, T. Xin, N. Lambert, D. Ruan, Y.-C. Cheng, F. Nori, F.-G. Deng, and G.-L. Long, npj Quantum Inf. 4, 52 (2018)
8. Quantum Anti-Zeno Effect without Rotating Wave Approximation, Q. Ai, Y. Li, H. Zheng, and C. P. Sun, Phys. Rev. A. 81, 042116 (2010)
9. Quantum Anti-Zeno Effect without Wave Function Reduction, Q. Ai, D. Xu, S. Yi, A. G. Kofman, C. P. Sun, and F. Nori, Sci. Rep. 3, 1752 (2013)