引入量子受限可在材料体系中产生丰富有趣的量子现象,通过这些量子现象可揭示受限(准)粒子的物理本质 [1]。例如,在石墨烯量子点中观测到的克莱因隧穿效应直接揭示了其载流子的相对论属性 [2]。更有趣的是,在量子受限情况下可以实现材料本身所不具备的新奇量子物态。例如,通常认为一个材料的贝里相位是一个常数,但在石墨烯量子点中,准粒子的贝里相位可利用磁场进行调控。因此我们可以通过贝里相位的改变来调控量子受限态的能级,实现一系列新奇量子物态 [3]。然而,能实现量子受限的有效方法并不多,在连续体系里,静电势是实验上几乎唯一可选的方法。在最近的工作中,何林教授课题组与合作者证明可以利用空间分布不均匀的赝磁场在石墨烯中实现量子受限,进一步施加外磁场时可实现具有谷差异的全新量子受限(两个谷中的载流子具有不同的受限尺寸和受限能级) [4]。
磁受限在理论上很早就已经被提出来了,然而倘若要实现100 meV大小的磁受限能级,则需要磁场强度在纳米尺度范围内变化数十特斯拉(图1(a)),这在实验上是难以实现的。虽然利用真实磁场很难实现,但何林教授课题组与合作者提出利用应变诱导的赝磁场可以实现类似的量子受限(图1(b))。赝磁场等效于真实磁场的轨道场,其大小和方向依赖于石墨烯的应变结构,可以在纳米尺度范围内变化几十甚至数百特斯拉 [5,6],因此可以利用空间分布不均匀的赝磁场在石墨烯中实现磁量子受限。更有趣的是,赝磁场在石墨烯的两个谷中大小相等但方向相反,当叠加一个真实磁场时,两个谷中载流子感受到的有效磁势垒将会不同,此时可实现具有谷差异的全新量子受限(图1(c))。
图1 (a)利用磁势垒实现磁受限的示意图。(b)利用赝磁场产生磁势垒实现磁受限的示意图。(c)利用赝磁场和真实磁场共同作用产生磁势垒实现具有谷差异的磁受限的示意图。
实验上,何林教授课题组利用衬底和石墨烯热膨胀系数的差异,在石墨烯中形成了准一维应变结构,应变较大和较小的结构交替出现(图2(a))。测量发现,在应变较大的区域有很强的赝磁场产生,并形成了赝朗道能级(图2(b)),而在应变较小的区域产生了几乎等间距的受限量子态(图2(c))。量子态的空间分布实验测量和理论分析结果均证明了这些受限态是由于空间不均匀的赝磁场形成的磁势垒产生的。进一步,他们在实验上施加了垂直外磁场,在量子受限区域观测到了谷差异的全新量子受限态(图2(d)左)。综合考虑周期性赝磁场产生的磁势垒和外加磁场的物理效应,理论计算非常好地模拟了具有谷差异的全新量子受限态(图2(d)右),并进一步指出两个谷的劈裂来源于其载流子感受到的不同磁势垒,从而使两个谷中的载流子有不同的空间受限尺寸(图2(e,f))。这一工作展示了利用赝磁场和真实磁场共同作用来实现新奇受限量子物态的可能性。
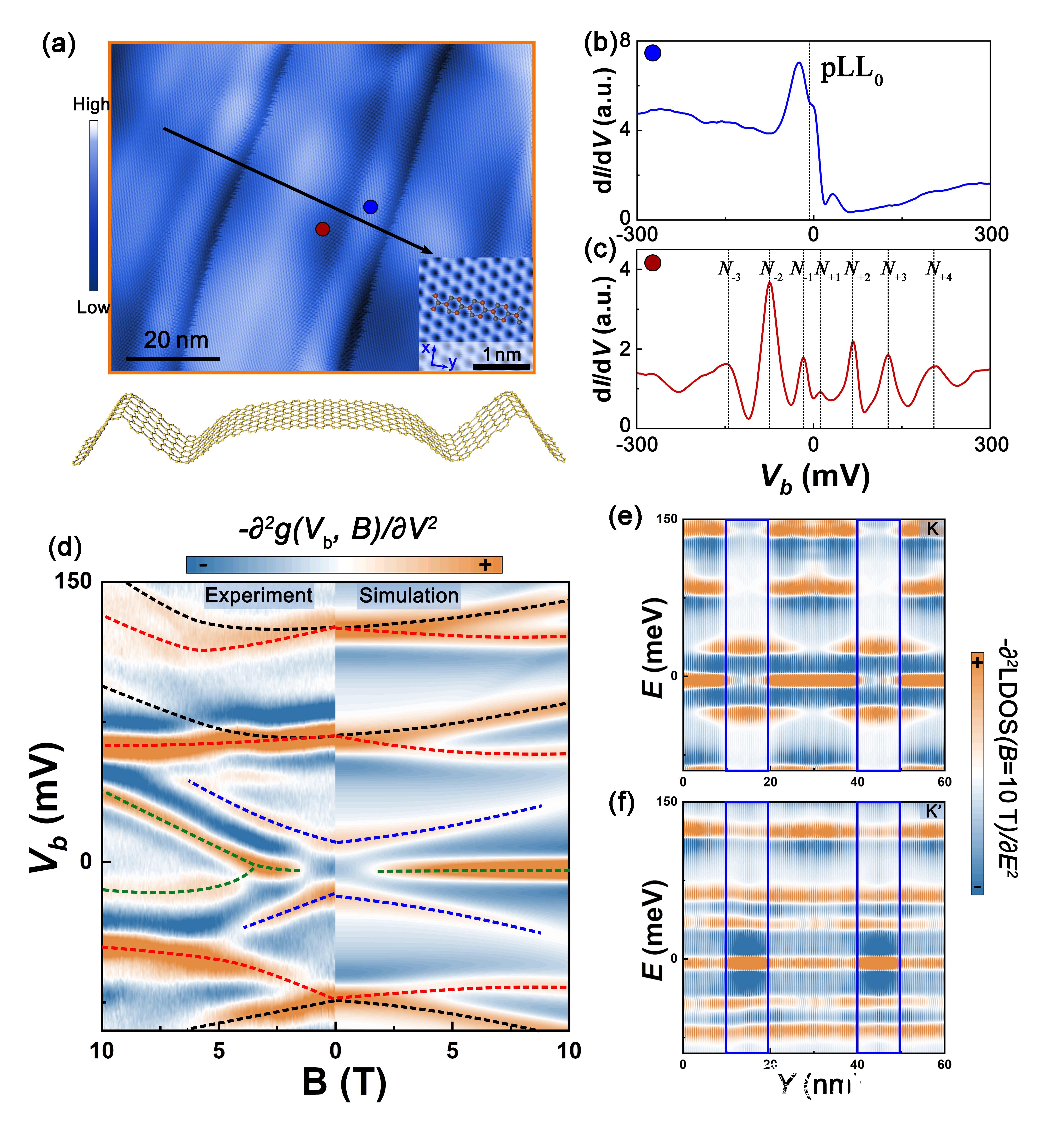
图2 (a)实验上测量的准一维周期应变结构。(b)在应变较大的区域探测到赝朗道能级。(c)在应变较小区域探测到磁受限导致的受限态。(d)左图:实验测量的受限态在磁场下的演化;右图:理论模拟的受限态在磁场下的演化。黑色和红色曲线分布表示两个谷中准粒子形成的受限态能级。 (e,f)赝磁场和真实磁场共同作用下,理论计算的两个谷中准粒子受限态的空间分布,可以清晰的看到此时实现了具有谷差异的磁受限。
相关成果近日以“Magnetic field-tunable valley-contrasting pseudomagnetic confinement in graphene”为题刊发在《Physical Review Letters》上 [4]。何林教授课题组博士生任雅宁为第一作者,北京大学孙庆丰教授课题组的博士生庄钰晨为该工作提供了理论计算,为文章的共同第一作者,北京大学的孙庆丰教授和北京师范大学的何林教授为本文通讯作者。
这项工作得到了国家自然科学基金委、国家重点研发计划、以及北京师范大学和北京大学的经费支持。
[1] S.-Y. Li*, L. He*, “Recent progresses of quantum confinement in graphene quantum dots”. Front. Phys. 17, 33201 (2022).
[2] Q. Zheng, Y. Zhuang, Q.-F. Sun*, L. He*, “Coexistence of electron whispering-gallery modes and atomic collapse states in graphene/WSe2 heterostructure quantum dots”. Nat. Commun. 13, 1597 (2022).
[3] Y.-N. Ren, Q. Cheng, Q.-F. Sun*, L. He*, “Realizing Valley-Polarized Energy Spectra in Bilayer Graphene Quantum Dots via Continuously Tunable Berry Phases”. Phys. Rev. Lett. 128, 206805 (2022).
[4] Y.-N. Ren, Y. Zhuang, Q.-F. Sun*, L. He*, “Magnetic field-tunable valley-contrasting pseudomagnetic confinement in graphene”. Phys. Rev. Lett. 129, 076802 (2022).
URL: https://link.aps.org/doi/10.1103/PhysRevLett.129.076802
DOI: 10.1103/PhysRevLett.129.076802
[5] Y.-W. Liu, Z. Zhan, Z. Wu, C. Yan, S. Yuan*, L. He*, “Realizing one-dimensional states in graphene via periodically coupled zeroth pseudo-Landau levels”. Phys. Rev. Lett. 129, 056803 (2022).
[6] S.-Y. Li, Y. Su, Y.-N. Ren, and L. He*, “Valley polarization and inversion in strained graphene via pseudo-Landau levels, valley splitting of real Landau levels, and confined states” Phys. Rev. Lett. 124, 106802 (2020).